SVM

间隔与支持向量

给定训练样本集$D= {(xi, y_i)}{i=1}^m, y_i \in {-1, +1}$，分类学习最基本的思想就是基于训练集D再样本空间中找到一个划分超平面，将不同类别的样本分开，但能将样本分开来的超平面可能有很多。例如：

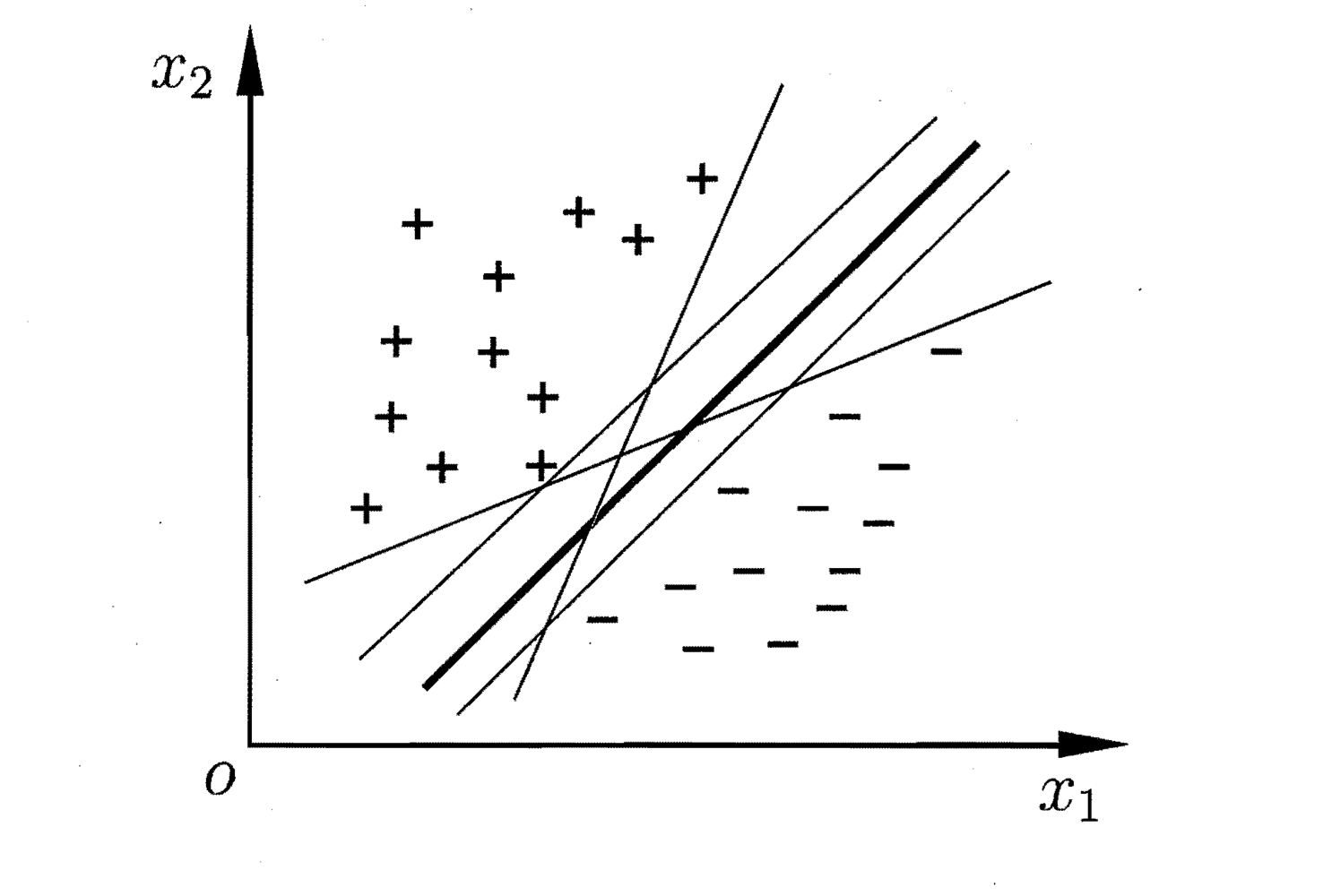
对于上图，直观上看，应该去找位于两类训练样本“正中间”的划分超平面，因为该划分超平面对训练样本局部扰动的“容忍”性最好。例如，由于训练集的局限性或噪声的因素，训练集外的样本可能比上图中的训练样本更接近两个类的分隔界，而红色的超平面受影响最小，因此其对未见示例的泛化能力最强。

在样本空间中，划分超平面可通过如下线性方程来描述：

$$w^T x + b = 0$$

其中$w = (w_1, w_2, \cdots, w_d)$为法向量，决定了超平面的方向，$b$为位移项，决定了超平面与原点之间的距离(其实二维平面上的直线$y = kx + b$本质上也是法向量的形式，其可以转换成$kx - y + b = 0$，即$(k, -1)(x, y)^T + b = 0$)。显然，划分超平面可被法向量$w$和位移$b$确定，下面我们将其记为$(w, b)$，样本空间中任意点$x$到超平面$(w, b)$的距离可写为:

$$r = \frac{|w^T x + b|}{||w||}$$

假设超平面$(w, b)$能将训练样本正确分类，即对$(x_i, y_i) \in D$，若$y_i = +1$，则有$w^T x_i + b > 0$(在超平面上方)；若$y_i = -1$，则有$w^T x_i + b < 0$(在超平面下方)。令

$$\begin{cases} w^T x_i + b \geq +1, y_i = +1 \\ w^T x_i + b \leq -1, y_i = -1 \end{cases} \tag{1} \\ 即找到那些使得所有样例到平面的距离都大于1的平面$$

可以证明，如果存在超平面$(w, b)$能将训练样本正确分类，则总存在缩放变换，使得上式成立，即总存在满足上式的超平面。下图是一个例子：

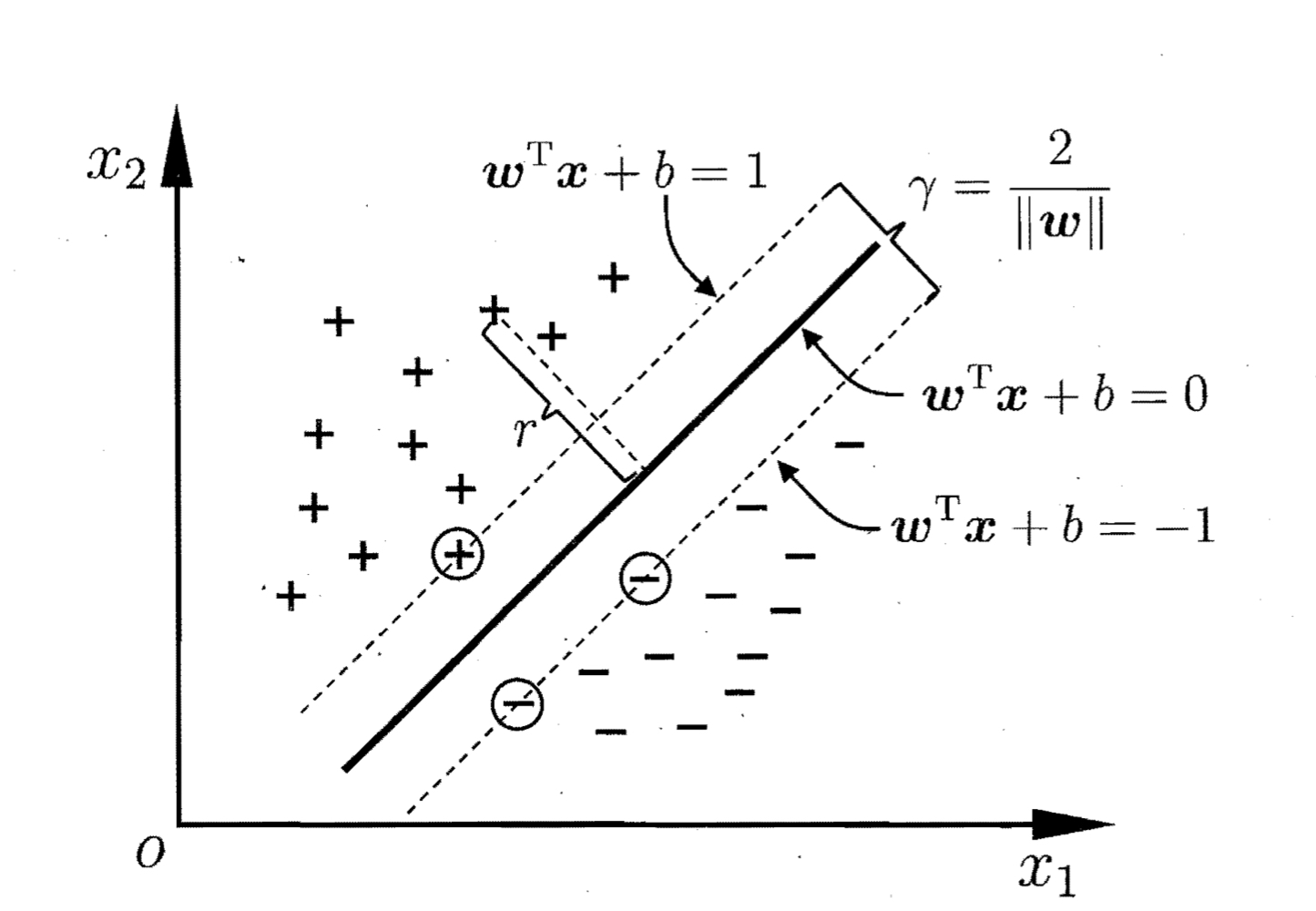
在上图中，距离超平面最近的几个训练样本点被称为“支持向量”，两个异类支持向量到超平面的距离之和称为“间隔”，在上图中，间隔为$\gamma = \frac{2}{||w||}$。

欲找到具有“最大间隔”的划分超平面，也就是要找到能满足(1)式约束的$w、b$，使得距离$\gamma$最大，即

$$max_{\{w,b\}} \frac{2}{||w||}，在满足约束y_i · (w^T x_i + b) \geq 1的条件下$$

显然为了最大化间隔，仅需要最大化$||w||^{-1}$，这等价于最小化$||w||^2$，于是，上式可重写为

$$min_{\{w, b\}} \frac{1}{2} ||w||^2，在满足约束y_i · (w^T x_i + b) \geq 1的条件下$$

这就是支持向量机的基本型