Padding

一般来说，如果我们对一个$n_h \times n_w$的图片用一个$k_h \times k_w$的卷积核进行卷积操作，那么输出图片的大小为$(n_h - k_h + 1) \times (n_w - k_w + 1)$。经过卷积操作之后，图片的大小会减小，同时，图片的边缘的信息也会被抹去。通常，一个卷积神经网络有好几层卷积层，如果不进行任何处理的话，那么经过多层卷积层之后，图片携带的信息可能就非常少了。

对输入图片进行Padding是一个常用的解决上面问题的方法。Padding即在图片周围填充额外的像素，通常，这些像素的值设置为0。如果我们对图像加入$p_h$行填充和$p_w$列填充，那么输出的图片的大小为$(n_h - k_h + p_h + 1) \times (n_w - k_w + p_w + 1)$

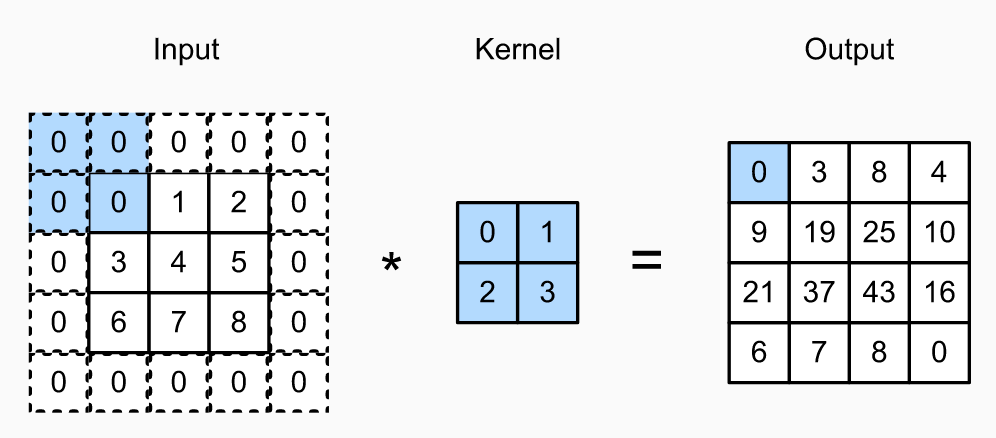
padding example

在许多情况下，通常会将$p_h$设置为$k_h - 1$，将$p_w$设置为$k_w - 1$，这样经过卷积之后的输出图片就和输入图片的大小一致。如果$k_h$为奇数(则$k_h - 1$为偶数)，那么一般就在输入图片的上面和下面都加上$\frac{k_h - 1}{2}$行填充，如果$k_h$为偶数(则$k_h - 1$为奇数)，那么可以在图片上方添加$\frac{k_h}{2}$行填充，在图片下方添加$(\frac{k_h}{2} - 1)$行填充，或者反过来。对于列填充来说也是这样的。

CNN中通常使用长和宽都为奇数的卷积核，使用奇数卷积核心可以保障在图片上下和左右添加的填充是均匀的。另外还有一个好处就是对于输出图片中的像素$Y[i, j]$来说，它正好是以输入图片中$X[i, j]$(注意输入图片的坐标以未添加padding的原始图片的左上角为原点)为中心周围像素的卷积运算的结果。

下面以一个8 x 8的输入图片，一个3 x 3的卷积核来做padding处理下的卷积代码示例：

import tensorflow as tf

conv2d = tf.keras.layers.Conv2D(1, kernel_size=3, padding='same')
# Here (1, 1) indicates that the batch size and the number of channels
input_tensor = tf.random.uniform(shape=(1, 8, 8, 1))
output_tensor = conv2d(input_tensor)
print(output_tensor.shape)

Stride

在之前的对图片进行卷积计算时，都是从图片左上角开始，每次向右移动一个像素，当一行计算完后，再往下移动一个像素。但是有些时候，为了计算效率和缩减采样次数，卷积窗口可以每次多向右或向下移动几个像素，跳过中间几个像素的计算。如下图：

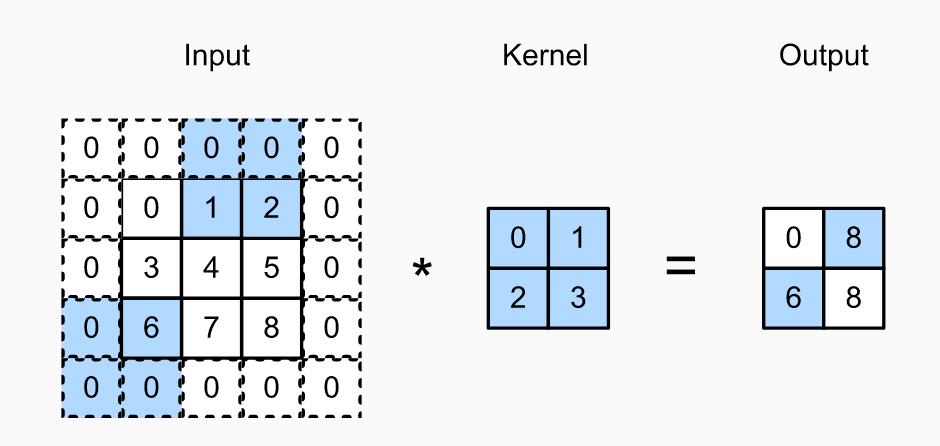
stride example
上图中的示例中，使用了水平2像素的stride，垂直3像素的stride。

假设输入图片的尺寸为$n_h \times n_w$，padding的尺寸为$p_h \times p_w$，卷积核的尺寸为$k_h \times k_w$，stride的尺寸为$s_h \times s_w$，则最终输出的结果的尺寸为$(n_h + p_h -k_h + s_h / s_h, \space n_w + p_w - k_w + s_w / s_w)$。

使用stride的代码示例：

1
2
3

conv2d = tf.keras.layers.Conv2D(1, kernel_size=3, padding='same', strides=2)
#or
conv2d = tf.keras.layers.Conv2D(1, kernel_size=(3, 5), padding="valid", strides=(3, 4))

通常来说，我们会将padding的长宽设置为相同的，stride的长宽也设置为相同的，即使用正方形的padding和stride。