成对使用new和delete时要采用相同形式

如果你在new表达式中使用[ ]，必须在相应的delete表达式中也使用[ ]。如果你在new表达式中不使用[ ]，一定不要在相应的delete表达式中使用[ ]。

另外尽量不要对数组形式做typedef动作，否则会导致new和delete的不匹配。例如：

1
2
3
4
5

typedef std::string Address[4];//用四个字符串来表示地址

std::string *pA = new Address;

delete pA;//应该使用 delete [] pA;

在资源管理类中提供对原始资源的访问

std中的shared_ptr和unique_ptr都提供了对原始资源对象的访问函数get()。在自己设计的资源管理类中也要提供一个访问原始资源的函数。

在资源管理类中小心copy行为

由于在资源管理类中存在指向动态内存的指针，在copy资源管理类时，动态资源的拷贝行为要根据实际情况来处理。所以需要对资源管理类的copy行为进行规定。

对于资管管理类的copy行为一般有以下几种处理办法：

• 禁止复制
• 使用引用计数法，通常只要内含一个shared_ptr成员变量即可
• 复制底部资源（深拷贝）
• 转移底部资源的拥有权

动态资源的copy属性决定了资源管理类的copy属性

以对象管理资源

该条款针中的资源指的是用户动态申请的资源。看一个例子：

假设有一个工厂函数，用于生产某特定的Investment对象

1
2
3
4
5
6
7
8
9
10
11
12

class Investment { ... };

Investment* createInvestment() {
  return new Investment();
}

int main() {
  ...;
  Investment* p = createInvestment();
  ...;
  delete p;
}

在上例中，如果用户不知道createInvestment的内部实现，那么就不知道Investment是动态创建出来的，另外如果用户知道createInvestment是动态创建出来的，也很有可能忘记了要delete。所以好的方式是利用非动态对象来管理动态申请的资源，利用非动态对象的析构函数来释放资源。

1
2
3
4
5

int main() {
  ...;
  std::shared_ptr<Investment> pInv(createInvestment());
  ...;
}

这种其实还有一个问题，就是用户很有可能忘记使用share_ptr来管理，所以最好直接让工厂函数返回一个shared_ptr。

1
2
3

std::shared_ptr<Investment> createInvestment() {
  return share_ptr<Investment>(new Investment());
}

通常使用shared_ptr和unique_ptr就可以完成对动态申请的资源进行管理，但是某些情况下可能需要自己设计一个用于管理动态资源的对象。

复制对象时勿忘记其每一个成分

如果自己不定义copy构造函数和copy assignment操作函数的话，编译器提供的copy构造函数和copy assignment操作符函数会自动对其基类部分进行copy构造和copy assign，但是如果自己定义了copy构造函数和copy assignment操作函数的话，那么就要在这两个函数中对基类进行复制。

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Base {
public:
  std::string name;
};

class Derived: public Base {
public:
  int age;
  //注意copy构造函数是在成员初始化列表中调用基类的copy构造函数
  //而copy assignment操作符函数是在函数体内调用基类的copy assignment操作符函数
  Derived(const Derived &another): Base(another), age(another.age) {};
  
  Derived& operator=(const Derived &another) {
    Base::operator=(another);
    age = another.age;
  }
}

令operator= 返回一个指向自身的引用

为了实现“连续赋值”，赋值操作符应该返回一个指向自身的引用。

1
2
3
4
5
6
7
8

class AClass {
public:
  void operator=(const AClass& aObject);//不能实现连续赋值
  AClass& operator=(const AClass& aObject);//可以实现连续赋值
};

AClass a, b, c;
a = b = c;//连续赋值

绝不在构造和析构过程中调用virtual函数

• 在derived class构造中的base class构造期，调用的virtual函数不会是派生类对应的实现，原因是因为虚表指针的初始化时机造成的。虚表指针会在进入到构造函数体之前被初始化，在进入到base class的构造函数体之前，虚表指针被赋值为指向base class的虚函数表，在进入到derived class的构造函数体内之前才会被赋值为指向derived class的虚函数表。
• 另外在derived class对象的base class构造期间，对象的类型是base class而不是derived class。若使用运行期类型信息例如dynamic_cast和typeid，也会把对象视为base class类型。

别让异常逃离析构函数函数

//说实话有点没懂这一点，有点

就是说在析构函数中就要对异常进行处理，不能rethrow？

为多态基类声明virtual析构函数

在使用c++多态特性的时候，通常会用基类指针或者基类引用来指向派生类对象，如果派生类对象是动态创建出来的，当delete的时候传入的是基类指针，如果析构函数是non-virtual的话，那么就可能出现属于派生类对象的部分未被析构的情况。因此，任何class只要带有virtual函数都几乎确定应该有一个virtual析构函数。

但是无端地将所有class的析构函数函数声明为virtual，也是错误的。在c++中所有STL容器如vector，list，set，map等都是不带virtual析构函数的class。

某些情况将析构函数声明为pure virtual函数

比如有时候你希望拥有抽象class，但是手上没有任何pure virtual函数时，可以将该类的析构函数声明为pure virtual函数，然而这里有个窍门：你必须为这个pure virtual析构函数提供一份定义，因为抽象class的析构函数仍会在派生类的析构函数中被调用，如果不提供定义，那么连接器就会报错。

总结

给base class一个virtual析构函数，这个规则只适用于有多态性质的base class

如果不想使用编译器自动生成的函数，就该明确拒绝

如果不想让编译器生成默认的copy构造函数和copy assignment函数，可以使用c++11的新特性

1
2
3
4
5

class UncopyableClass{
public:
  UncopyableClass(const UncopyableClass& uncopyableClass) = delete;
  UncopyableClass& operator=(const UncopyableClass& uncopyableClass) = delete;
};

了解C++默认编写并调用了哪些函数

在class中，如果你自己没声明，编译器会为一个类自动声明(编译器版本的)一个默认构造函数，一个copy构造(拷贝构造)函数和一个copy assignment(拷贝赋值)操作符函数，这些函数都是public且inline的。但是只有当这些函数被调用了，它们才会被编译器创建出来。另外编译器还会提供一个默认的析构函数，这个析构函数是non-virtual的，除非这个class的base class自身声明有virtual 析构函数。

对于编译器提供的copy构造函数和copy assignment操作符函数，都只是单纯地将来源对象的每个non-static成员变量进行浅拷贝到目标对象。

某些情况下即使你自己未声明copy assignment操作符函数，编译器也会拒绝提供

• class内含reference成员
• class内含const成员
• Base class将copy assignment操作符声明未private，编译器将拒绝为其derived class生成一个copy assignment操作符

间隔与支持向量

给定训练样本集$D= {(xi, y_i)}{i=1}^m, y_i \in {-1, +1}$，分类学习最基本的思想就是基于训练集D在样本空间中找到一个划分超平面，将不同类别的样本分开，但能将样本分开来的超平面可能有很多。例如：

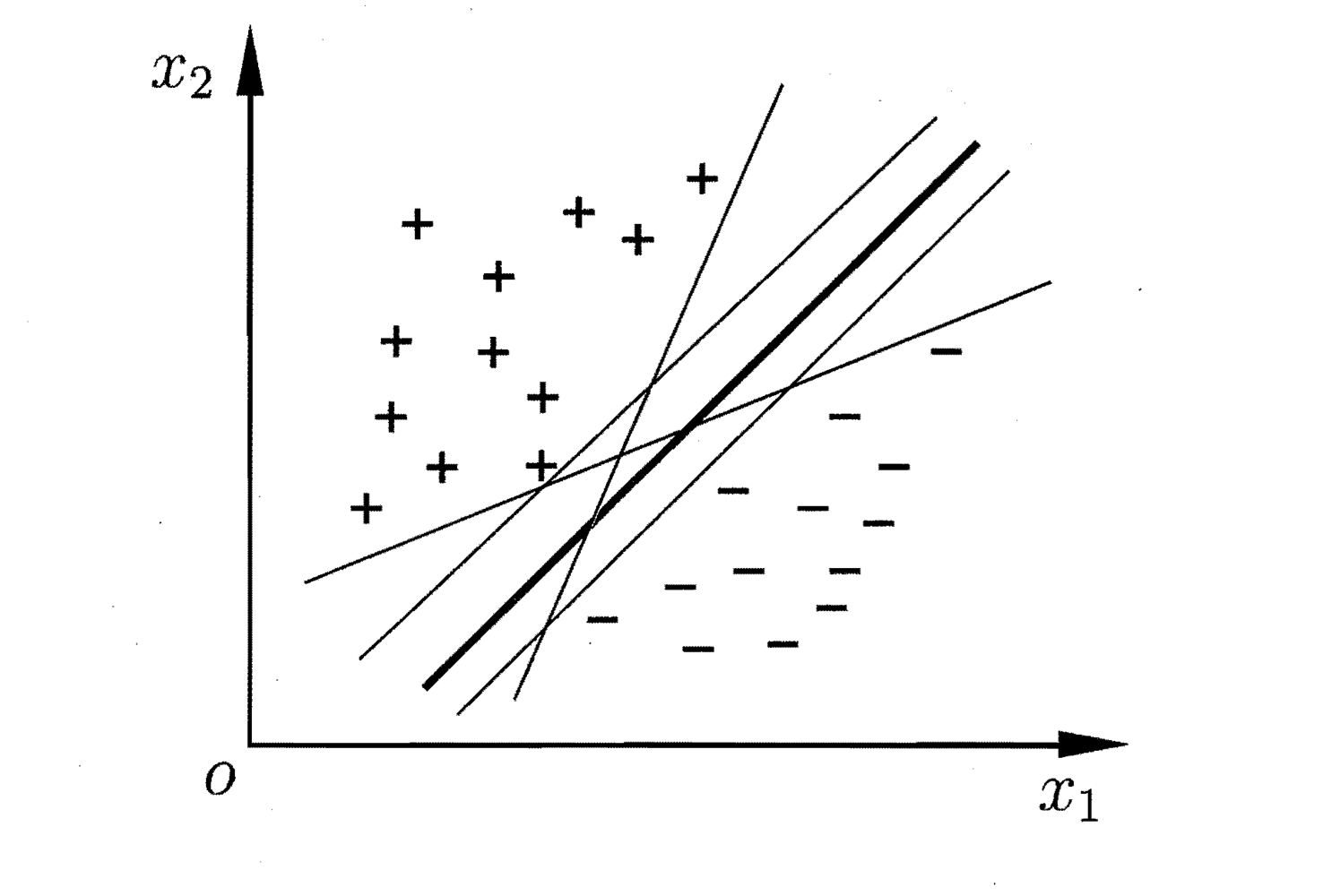
对于上图，直观上看，应该去找位于两类训练样本“正中间”的划分超平面，因为该划分超平面对训练样本局部扰动的“容忍”性最好。例如，由于训练集的局限性或噪声的因素，训练集外的样本可能比上图中的训练样本更接近两个类的分隔界，而粗线的超平面受影响最小，因此其对未见示例的泛化能力最强。

在样本空间中，划分超平面可通过如下线性方程来描述：

其中$w = (w_1, w_2, \cdots, w_d)$为法向量，决定了超平面的方向，$b$为位移项，决定了超平面与原点之间的距离(其实二维平面上的直线$y = kx + b$本质上也是法向量的形式，其可以转换成$kx - y + b = 0$，即$(k, -1)(x, y)^T + b = 0$)。显然，划分超平面可被法向量$w$和位移$b$确定，下面我们将其记为$(w, b)$，样本空间中任意点$x$到超平面$(w, b)$的距离可写为:

假设超平面$(w, b)$能将训练样本正确分类，即对$(x_i, y_i) \in D$，若$y_i = +1$，则有$w^T x_i + b > 0$(在超平面上方)；若$y_i = -1$，则有$w^T x_i + b < 0$(在超平面下方)。令

即找到那些使得所有样例到平面的距离都大于1的平面

可以证明，如果存在超平面$(w, b)$能将训练样本正确分类，则总存在缩放变换，使得上式成立，即总存在满足上式的超平面。下图是一个例子：

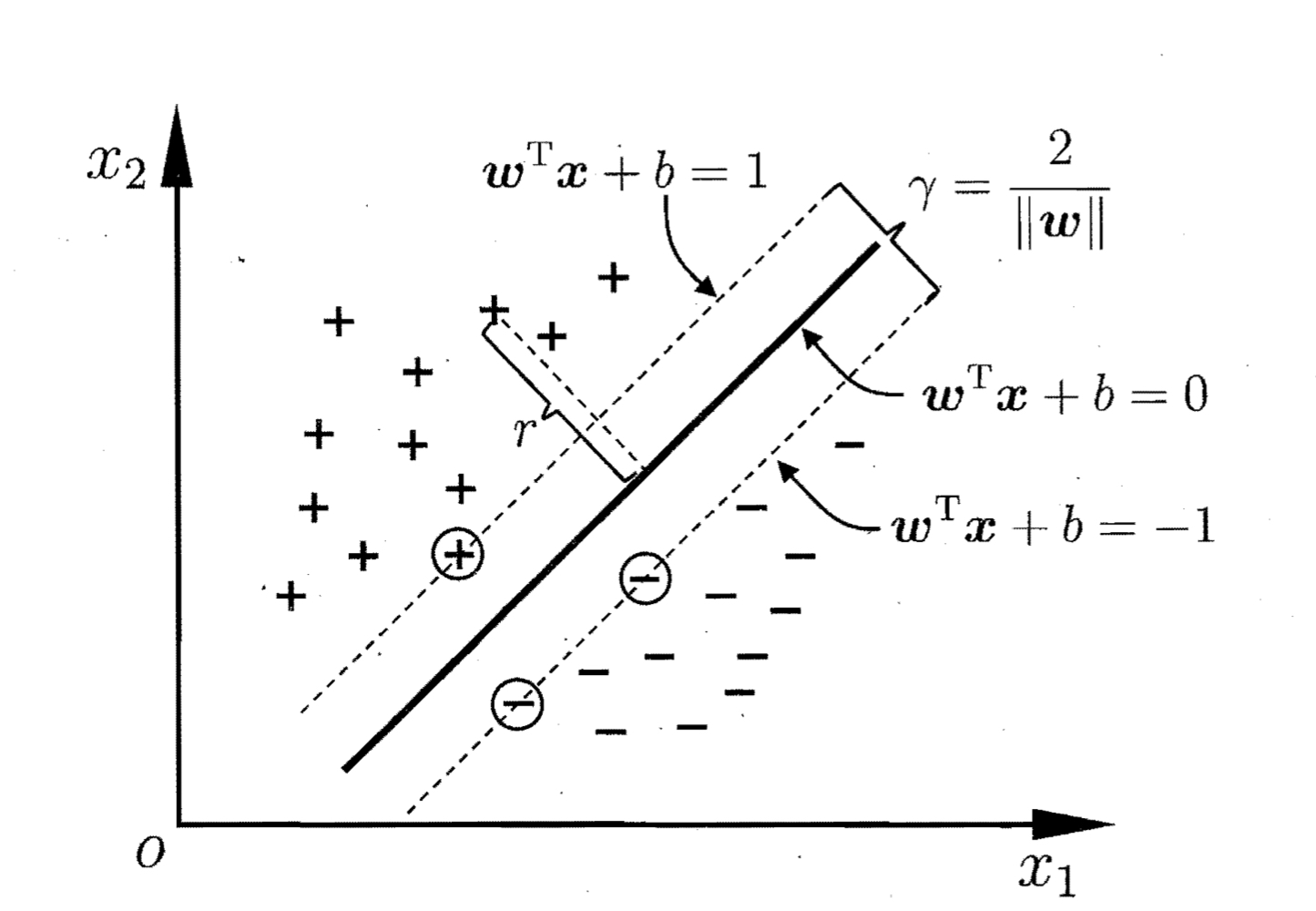
在上图中，距离超平面最近的几个训练样本点被称为“支持向量”，两个异类支持向量到超平面的距离之和称为“间隔”，在上图中，间隔为$\gamma = \frac{2}{||w||}$。

欲找到具有“最大间隔”的划分超平面，也就是要找到能满足(1)式约束的$w、b$，使得距离$\gamma$最大，即

显然为了最大化间隔，仅需要最大化$||w||^{-1}$，这等价于最小化$||w||^2$，于是，上式可重写为

这就是支持向量机的基本型