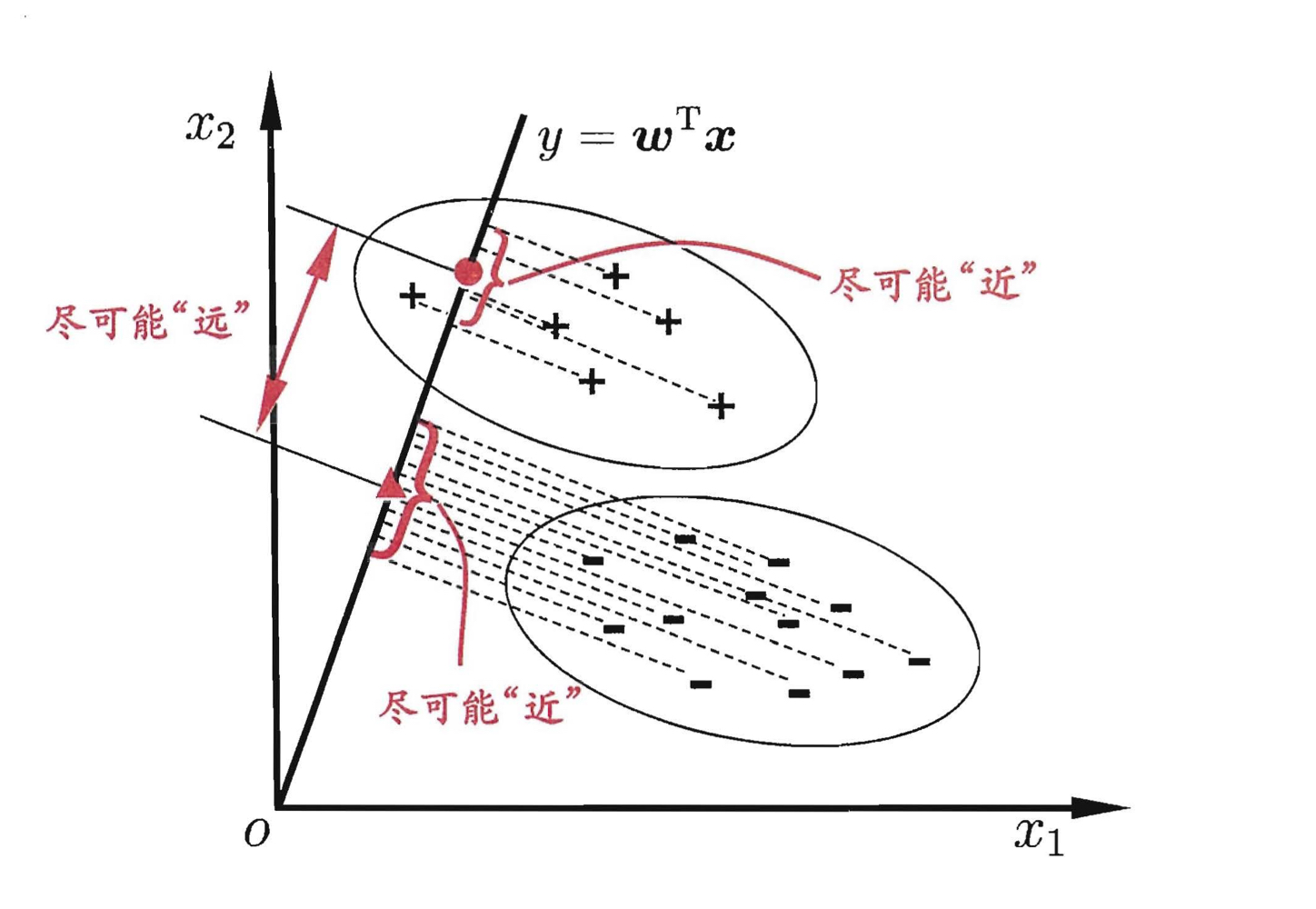
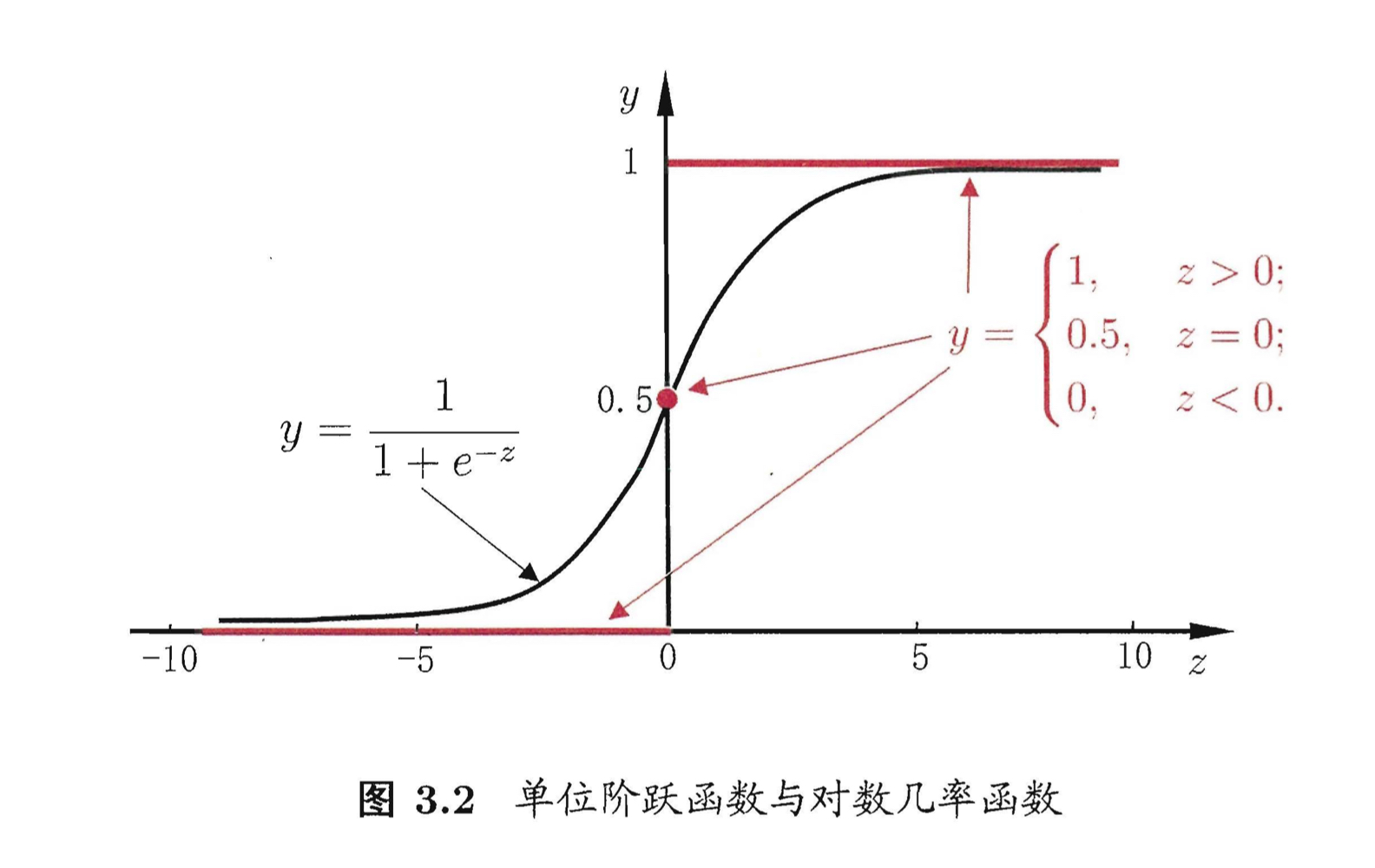
从二分类到多分类

在遇到多分类任务时，有些二分类学习方法可直接推广到多分类，例如线性判别分析LDA，但在更多情形下，我们是基于一些基本策略，利用二分类学习器来解决多分类问题。

一般的，对于N个类别$C_1, c_2, \cdots,C_N$，多分类学习器的基本思想是拆解法，即将多分类任务拆为若干个二分类任务求解。在测试时，对这些二分类器的预测结果进行集成以获得最终的多分类结果，比如说可以选择概率最大的那个结果。

拆分策略

OvO策略

给定数据集$D={(xi y_i)}{i=1}^{m}$，$y_i \in {C_1, C_2, \cdots, C_N }$，OvO将这N个类别两两配对，从而产生$\frac{N(n-1)}{2}$

个二分类任务。在一个二分类任务中，把一种类别当做正例(随便选定两者中的一个)，另一种类别当做负例。

在测试阶段 ，新样本将同时提交给所有分类器，将会得到$\frac{N(N-1)}{2}$个分类结果，最终结果结果可通过投票产生：即把被预测得最多的类别作为最终结果。

OvR策略

对于OvR，则是每次将一个类别的样例作为正例，所有其他类的样例作为反例来训练N个分类器。在测试时，若仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果；若有多个分类器预测为正类，则通常考虑各分类器的预测置信度，选择置信度最大的类别作为分类结果。

OvO于OvR策略比较

OvR相比于OvO只需要训练N个分类器，而OvO需训练$\frac{N(N-1)}{2}$个分类器，因此，OvO的存储开销和测试时间开销通常比OvR更大。但在训练时，OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvR更小。至于预测性能，则取决于具体的数据分布，在多数情况下两种策略差不多

MvM

MvM是每次将若干个类作为正类，若干个其他类作为反类。MvM的正、反类构造必须有特殊的设计，不能随意选取。有一种常用的MvM技术：纠错输出码(Error Correcting Output Codes, ECOC)。

纠错输出码ECOC

ECOC工作过程主要分为两步：

• 编码：对N个类别分别做M次划分，每次划分将一部分类别划分为正类，一部分划分为反类，从而形成一个二分类训练集；这样一共产生M个训练集，可以训练出M个分类器。
• 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码。将这个编码与每个类别各自的编码进行比较，返回其中距离(海明距离或者欧式距离)最小的类别作为最终预测结果

类别划分通过编码矩阵指定，编码矩阵有多种形式，常见的主要有二元码和三元码。二元码将每个类别分别指定正类和反类；三元码在正、反类之外，还可指定停用类。

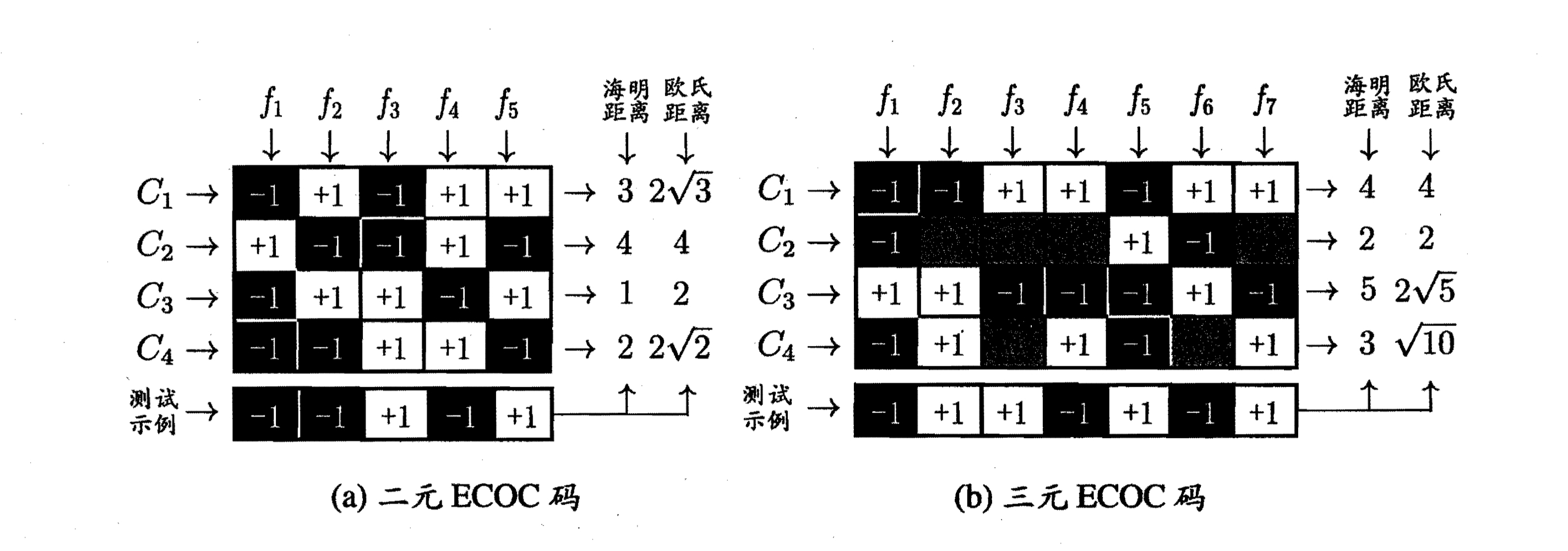
在编码矩阵中，使用“+1”、“-1”分别表示正、反例，0表示不使用该类样本即停用类。在上图的例子中，(a)图中的测试用例最后分类结果应归为$C_3$类，(b)图中的测试用例最后分类结果应归为$C_2$类。

为什么叫做“纠错输出码”呢？原因是在测试阶段，ECOC编码对分类器的错误有一定的容错和纠正能力。例如，图(a)中对测试用例的正确预测编码是$(-1,+1,+1,-1,+1)$，假设在预测时某个分类器出错了，假设$f_2$分类器出错了，从而导致了错误的编码$(-1,-1,+1,-1,+1)$，但基于这个编码仍能产生正确的最终分类结果$C_3$。一般来说，对同一个学习任务，ECOC编码越长，纠错能力越强。然而，编码越长意味着所需训练的分类器越多，计算、存储开销都会增大；另一方面，对有限类别数，可能的组合数目是有限的，码长超过一定范围后就失去了意义。

对于等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强。因此，在码长较小时可根据这个原则计算出理论最优编码。然而一般很难求的最优的编码，选择一个较优的编码就足够了。

思路

线性判别分析(Linear Discriminant Analysis, LDA)是一种经典的线性分类学习方法。LDA的思想非常朴素：给定训练集样例，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

模型求解

模型推广到多分类任务

总结

什么是logistic回归

logistic回归又叫做对数几率回归，它是基于线性模型的一种分类模型。那么如何用线性回归得到的输出进行分类任务呢？只需找一个单调可微的函数将分类任务的真实标记y与线性回归模型的预测值联系起来。单调可微的目的是为了方便模型的求解。

例如对于二分类任务，其输出标记$y \in {0, 1}$，而线性回归模型产生的预测值$z = wx + b$是实值，于是，我们需要将实值转换为0/1值。最理想的是单位阶跃函数：

即若预测值$z$大于0就判为正例，小于0则判为反例，预测值为临界值0则可任意判别。

但是，单位阶跃函数不连续，所以直接使用单位阶跃函数的话，该分类模型则将很难求解。

由于不能使用阶跃函数，所有我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”，并希望它单调可微。对数几率函数(logistic function)正是这样一个常用的替代函数：

阶跃函数和对数几率函数的图像为：

从上图可以看出，对数几率函数是一种”Sigmoid函数”(即形似S的函数)，对率函数是Sigmoid函数中最重要的代表。

将线性模型和对数几率函数结合得到最后的logistic回归的模型：

logistic模型求解

logistic模型求解就是求出最优的$w$和$b$。然而这里不能直接使用求解线性回归的方法进行求解，即不能定义目标函数为$argmin{(w,b)}\sum{i=1}^{m}(wx_i+b - y_i)^2$。因为在这里，数据集中的y只能取0和1(对于二分类来说)，如果仍然使用均方误差来作为损失函数的话，那么在这里均方误差函数将不再是一个凸函数，所以我们要寻求另外的目标函数。

logistic回归中的对率函数的实际输出其意义为：样本为正例(即$y=1$)的概率。例如对于某个样例$x$，在参数为$w,b$的条件下的输出为0.7，则表示该样例有0.7的概率为正例。相反如果输出为0.3，则表示该样例为正例的概率为0.3，即为反例的概率有0.7。

则由此即有：

于是，可通过极大似然法来估计$w$和$b$。给定数据集${(xi, y_i)}{i=1}^{m}$，其中$y_i \in {0,1}$，则可得极大似然函数为：

其中$p(y_i|x_i,w,b)$可改写为$y_ip(y=1|x_i,w,b) + (1-y_i)p(y=0 | x_i,w,b)$，则似然函数可写为：

由于似然函数法的思想就是求出使得得出当前结果的概率最大的参数，$l(w,b)$的意义其实就是在参数为$w$和$b$的条件下，取值为当前数据集的y的概率再取对数。由于对数函数和原函数具有相同的单调性，当对数函数取最大值时，原函数也去最大值。所以最后我们的目标函数即为：

注意是argmax。

最大化(1)式，等价于：

公式(2)是最常用的形式。这个公式相当于在说当$y_i = 1$时，损失函数为$ln\frac{1}{1 + e^{-(wx+b)}}$，当$y_i = 0$时，损失函数为$1-ln\frac{1}{1 + e^{-(wx+b)}}$。接下里就是利用梯度下降法或者其他方法求解最优解即可了。

利用极大似然估计法寻找目标函数也是常用的一种方法。

总结

logistic回归虽然它的名字是“回归”，但实际上却是一个分类学习方法。这种方法有很多特点，它是基于线性回归模型的，具有很好的解释性。同时它是直接对分类可能性进行建模，无需要事先假设数据分布，这样就避免了假设分布不准确所带来的问题。

它不仅是预测出类别，而是可得到近似概率预测。此外，对率函数是任意阶可导的凸函数。

离散型

0-1 分布B(1, p)

$E(x) = p$，$D(x) = p(1-p)$

二项分布B(n, p)

$E(x) = np$，$D(x) = np(1-p)$

泊松分布$P(\lambda)$

$E(x) = \lambda$，$D(x) = \lambda$

几何分布a(p)

$E(x) = \frac{1}{p}$，$D(x) = \frac{1 - p}{p^2}$

几何分布的意义表示一个事件首次发生所需要的实验次数

超几何分布H(n, N, M)

$E(x) = \frac{nM}{N}$，超几何分布的意义为：在N件产品中有M件不合格，在产品中随机取出n件检查，发现有k件不合格的概率。

连续型

均匀分布U(a,b)

$E(x) = \frac{a+b}{2}$，$D(x) = \frac{(b-a)^2}{12}$

指数分布$E(\lambda)$

$E(x) = \frac{1}{\lambda}$，$D(x) = \frac{1}{\lambda^2}$

正态分布$N(\mu, \sigma^2)$

$E(x) = \mu$，$D(x) = \sigma^2$

C++ 编译链接过程

1、预处理器：将.c 文件转化成 .i文件，使用的gcc命令是：gcc –E，对应于预处理命令cpp；

2、编译器：将.c/.h文件转换成.s文件，使用的gcc命令是：gcc –S，对应于编译命令 cc –S；

3、汇编器：将.s 文件转化成 .o文件，使用的gcc 命令是：gcc –c，对应于汇编命令是 as；

4、链接器：将.o文件转化成可执行程序，使用的gcc 命令是： gcc，对应于链接命令是 ld；

5、加载器：将可执行程序加载到内存并进行执行，loader和ld-linux.so。

由不同编译器创建的二进制模块很可能无法正确链接，在链接编译模块时，请确保所有对象文件或库都是由同一个编译器生成的（或同一标准的编译器）

编译器前端和后端

编译器粗略分为词法分析，语法分析，类型检查，中间代码生成，代码优化，目标代码生成，目标代码优化。

把中间代码生成及之前阶段划分问编译器的前端，那么后端与前端是独立的。后端只需要一种中间代码表示，可以是三地址代码或四元式等，而这些都与前端生成的方式无关。

编译器的前端将不同的高级编程语言经过词法分析、语法分析转化为与前端语言无关的中间表示。有了与前端语言无关的中间表示，一个编译器就可以支持编译多种高级语言。

按照这个分类，自己动手编写编译器，可以不必从头开始了。使用LLVM，我们可以做一个前端，然后和LLVM后端对接。

大端（Big Endian/Big Endiayin）

数据的高字节部分放在内存中的低字节地址，数据的低字节部分放在内存中的高字节地址

例如：

小端（Little Endian）

数据的高字节部分放在内存中的高字节地址，数据的低字节部分放在内存中的低字节地址

例如：

类型转换

不同基本操作数进行运算会隐式的将内存占用较少的类型转换成占用较多的操作数类型

尽量不要使用隐式类型转换，即使是隐式的数据类型转换是安全的，因为隐式类型数据转换降低了程序的可读性。尽量使用强制（显示）类型转换

将占用空间大的数据的指针强制转换成占用空间小的数据的指针，会发生内存截断，将占用空间小的数据的指针强制转换成占用空间大的数据的指针，会发生内存扩张。例如

1
2
3
4
5
6
7

doule d5 = 100.0;

int *pInt = (int*)&d5;

int i4 = 100;

double pDbl = (double*)&i4;

内存截断：

内存扩张：

发生内存扩张时，往扩张的内存写数据会发生运行时错误

标识符

引用类型

引用变量在声明时必须被赋值，引用变量和被引用的变量的地址是相同的

1
2
3
4

int a = 1;
int &b = a;
printf("the address of a is %p and the address of b is %p", &a, &b);
//打印的结果地址相同

常量

对于指针类型和引用类型，将非const值赋值给const变量是合法的，但是反之则是非法的

1
2
3
4
5
6
7

int a = 10;

const int &b = a; //ok

int &c = b;//错误，const int &类型，不能直接赋给int &类型

int *d = &b;//错误，const int *类型，不能直接赋给int *类型

字面常量

字面常量：直接出现的数字、字符、字符串等，只存在基本数据类型的字面常量，字面常量只能引用，不能修改。除字符串外，你无法取一个字面常量的地址，例如：

1

int *p = &5;//语句错误

并且当你试图通过常量字符串的地址修改其中的字符时就会报告“只读错误”（此错误为运行时错误）例如：

1
2
3

char *pChar = "abcdef";

*(pChar + 2) = 'k';//错误，不能修改字面常量的内存单元

符号常量

符号常量分为用#define定义的宏常量和用const定义的常量。

使用#define宏定义的符号常量在进入编译阶段前就已经被替代为所代表的字面常量了，因此宏常量本质上是字面常量。

1
2
3
4
5
6
7

const long lng = 10;

long *pl = (long *)&lng;

*pl = 11;

std::cout<<lng<<"-"<<*pl;//输出为10-11

1
2
3
4
5
6
7
8
9
10
11
12
13
14

struct Integer {
    int m_lng
}


const Integer int_1;

//int_1.m_lng = 1000;//编译错误

Integer *pInt = (Integer *)&int_1;

pInt->m_lng = 1000;

std::cout << int_1.m_lng << "-" << pInt->m_lng;//输出为1000-1000

指针运算

• 指针自增（++），表示它指向了序列中的后一个元素

• 指针自减（—），表示它指向了序列中的前一个元素

• 指针加一个正整数i，表示它向后递进i个元素

• 指针减一个正整数i，表示它向前递进i个元素

• 两个同类型指针相减，表示计算它们之间的元素个数

指针加/减一个正整数i，其含义并不是在其值上直接加/减i，还要包含所指对象的字节数信息。

不能对void*类型指针使用“*”来取所指的变量

数组

任何数组，不论是静态声明的还是动态创建的，其所有元素在内存中都是连续字节存放的，也就是说保存在一大块连续的内存区中，std::vector的所有元素对象在内存中也是连续存放的。

创建动态二维数组的方法

1
2
3
4
5
6
7

int **p = new int*[n];

for(int i = 0; i < n; ++i) {

p[i] = new int[m];

}

一个很不符合逻辑的表达式

1
2
3
4
5
6
7

int a = 0;

int b = 1;

int c = 2;

a + b = c;//这句话会先执行a+b，将a+b的值放在一个临时对象中，然后将c的值赋予该临时对象。

最后一个表达式没有任何实际意义，它一般是错误将判断相等表达式“==”错误写成“=”的结果

endl

endl是一个函数模板，它实例化之后变成一个模板函数，其作用是插入换行符并刷新输出流。其中刷新输出流指的是将缓冲区的数据全部传递到输出设备并将输出缓冲区清空。

避免头文件循环引用

1
2
3
4
5
6
7

#ifndef HEADER_H

#define HEADER_H

//place include file content and your code here

#endif

宏

• #ifdef 只判断是否定义了某个宏

• #if 不仅判断是否定义了宏，而且还判断宏是否为真

• #undef 用于取消定义的宏

利用宏转字符串

1

#define TO_STR(a) #a

在宏定义汇总使用#表示将符号转换为对应的字符串，例如使用上面的宏TO_STR(test)的结果就是"test"。

利用宏链接符号

1

#define Contact(a) a##_1

在宏定义中使用##表示连接，例如使用上面的宏Contact(test)的结果就是test_1。

常微分方程

方程的解为相若$y=f(x)$的，只有一个自变量的微分方程，称为常微分方程，如果有多个自变量，则称为偏微分方程。

可分离变量型

形如$y’ = g(x)$的微分方程，为可分离变量型的常微分方程。

其解法为：

可转化为可分离变量型

形如$y’ = g(ay+bx+c)$的微分方程，可以转化为可分离变量型的微分方程

解：

​ 令

​ 则

​ 则原式变为：

​ 即转化为了可分离变量型

齐次常微分方程

形如$\frac{dy}{dx} = g(\frac{y}{x})$或$\frac{dx}{dy} = g(\frac{x}{y})$的微分方程称为0次齐次常微分方程，其解法为：

解：

​ 令

​ 则：

​ 也转换为了可分离变量型的微分方程了。

一次线性常微分方程

1、$y’ + p(x)y = q(x)$

其解的公式为：

2、$y’ + p(x)y = q(x)y^n$

解：

​ 原式两边同除$y^n$

​ 令

​ 则有

​ 则原式转换为：

​ 再直接使用公式(1)即可。

二次微分方程

可降次二次微分方程

1、$y’’ = g(y’, x)$

解：

​ 令

​ 则

​ 则原式转换为：

2、$y’’ = g(y’, y)$

解：

​ 令

​ 则

​ 则原式转换为：

二次常系数微分方程

形如$y’’+py’ + qy = g(x)$，其中$p,q$为常数的微分方程称为二次常系数微分方程。

二次常系数齐次微分方程

如果二次常系数微分方程中g(x) = 0，则称该方程为二次常系数齐次微分方程。其通解取决于其对应的特征方程的解的个数。

若有$y’’+py’ + qy = 0$，其对应的特征方程为$\lambda^2 + p\lambda + q = 0$，则其通解为：

其中$C_1、C_2$为任意常数

二次常系数非齐次微分方程

二次常系数非齐次微分方程的解的结构为其对应的齐次微分方程的通解再加上非齐次微分方程对应的一个特解。

一般考察的非齐次方程有两种：

1、$g(x) = P_n(x)e^{ax}$，$P_n(x)$为x的n次多项式

其特解公式为：

$Q_n(x)$为x的n次多项式

2、$g(x) = e^{ax} [P_n(x)cosbx + Q_m(x)sinbx]$，$h_n$为x的n次多项式，$h_m$为x的m次多项式

其特解公式为：

$h_s(x)$为x的s次多项式，其中s = $max{m, n}$

要求出多项式的具体参数，就将特解带回原方程求解即可

欧拉方程

$x^2 \frac{d^2y}{dx^2} + px \frac{dy}{dx} + qy = f(x)$，其中$p、q$为常数，这种方程即为欧拉方程。

解：

​ 对于 x>0，令

​ 则

​ 则

​ 则原式转换为：

​ 即转化为了二次常系数微分方程。

​ 同理对于x < 0，也可以用同样的方法。

介值定理

1、如果函数$f(x) \in C[a,b]$，即在$(a,b)$上连续，则存在$\eta \in (a,b)$，使得$f(\eta)$介于$f(a)$与$f(b)$之间。

2、如果函数$f(x) \in C[a,b]$，且在$f(x)$在$[a,b]$上取得最小值min，最大值max，则存在$\eta \in (a,b)$，使得$f(\eta) in [min, max]$。

费马定理

若函数$f(x)$一阶可导，且在点$x_0$出取得极值，则$f’(x_0) = 0$

罗尔中值定理

若函数$f(x) \in C[a,b]$，且$f(a)=f(b)$，则存在$\eta \in (a,b)$，使得$f’(\eta) = 0$

洛尔定理的推广：

1、//TODO: finish this part

拉格朗日中值定理

若函数$f(x) \in C[a,b]$，则存在$\eta \in (a,b)$，使得$f(b) - f(a) = f’(\eta)(b-a)$。

证明：

构造函数$F(x) = [f(b) - f(a)]x - (b-a)f(x)$，则有$F(a) = F(b)$，则根据罗尔中值定理可证得。

柯西中值定理

如函数$f(x) \in C[a,b], g(x) \in C[a,b]$，则存在$\eta \in (a,b)$，使得:

证明：

构造函数$F(x) = f(x)[g(b) - g(a)] - f(x)[f(b) - f(a)]$ ，然后有$F(a) = F(b)$，则根据罗尔中值定理可证得。

积分中值定理

若$f(x)$在$[a,b]$上可积分，则存在$\eta \in (a,b)$，使得$f(\eta)(b-a) = \int_{a}^{b} f(x)dx$

推广的积分中值定理

设$f(x)$，$g(x)$在$[a,b]$上连续，且$g(x)$在$[a,b]$上不变号，则存在$\eta \in (a,b)$，使得$\int{a}^{b} f(x)g(x)dx = f(\eta) \int{a}^{b}g(x)dx$

证明：

设$F(x) = \int{a}^{x} f(t)g(t)dt$，$G(x) = \int{a}^{x}g(t)dt$，在$(a,b)$上使用柯西中值定理即可证得。

基本形式

给定d个特征描述的示例$x=(x_1, x_2, \cdots, x_d)$，其中$x_i$是$x$在第$i$个特征上的取值，线性模型是试图学得一个通过属性的线性组合来进行预测的函数，即

在线性模型中$w$直观表达了个属性在预测中的重要性，因此线性模型有很好的可解释性。

线性回归

给定数据集$D = {(x_1,y_1),(x_2,y_2), \cdots, (x_m,y_m)}$，其中$x_1$为d个特征描述的d维向量。线性回归试图学得

那么如何衡量尽可能接近呢？均方误差是回归任务重最常用的性能度量，因此我们可试图让均方误差最小化，即

$(w^*,b^*)$表示$w$和$b$的解。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”，在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

单特征求解

对于只有一个特征的线性回归模型的最小二乘法的解方法为：

令

分别对w和b求偏导

令偏导数为0 可解得$w$和$b$为

式(4)可由式(2)等于0直接得出，式(3)可有式(2)和式(4)联立推出。其中$\overline x = \frac{1}{m} \sum_{i=1}^{m}x_i$为$x$的均值。

多元线性回归

上面对只有一个特征描述的数据集如何使用最小二乘法求解线性回归问题进行了说明，然而实际的问题更一般的情况是有多个特征标记的数据。这种称为多元线性回归。

为了便于讨论多元线性回归中$w$和$x$都为向量的情况，我们将$b$吸收进入$w$，即令$\hat w = (w;b)$，$\hat w$是一个$(d+1) \times 1$的矩阵。把数据集$D={(xi, y_i)}{i=1}^{m}$(注意$x_i$为向量，$y_i$为标量)表示为一个$m \times (d + 1)$大小的矩阵$X$，其中每行对应一个示例，每行的前d个元素对应一个示例的d个特征取值，最后一个元素恒置为1。并且把所有示例的最后结果表示为一个$m \times 1$的矩阵$Y$

即：

则

则我们的目标是

$Y-X \hat w$为一个$m \times 1$的矩阵。

同理为了求出$\hat w$，可以对$\hat w$求导并令其等于0，注意这里是标量对向量求导，具体标量如何对向量求导的可以看我的另一篇博客。

令$E_{\hat w} = (Y - X\hat w)^T(Y - X\hat w)$，对$\hat w$求导得到：

(其中$dX$、$dY = 0$)

令式(5)等于0可得：

最后得到的线性回归模型为：

这里求解模型的方法其实就是标准方程法。

对于线性规划问题，另外的一种解法就是梯度下降。

一个小问题：若$X^TX$不可逆

如果出现了$X^TX$不可逆的情况，可能是一下问题导致的：

1、选用的特征有冗余的特征，即一个特征可以同其他几个特征线性表示

2、用于训练的数据的数量小于选用的特征数量

如果仍然还是不可逆，那么可以对矩阵求伪逆，事实上在编程时大多数矩阵操作运算的库都提供了求矩阵伪逆的函数。

或者直接使用求解线性方程的方法，求出多个$\hat w$，他们都能使均方误差最小化，选择哪一个作为最后的输出将由学习算法的归纳偏好决定，常见的做法是引入正则化。

对比一下梯度下降法和标准方程法

综上所述，当n比较小时，可以考虑使用标准方程法，当n很大时，使用梯度下降法会比较好

三角函数族

傅立叶级数

对于一个周期函数，它都能展开为三角函数的级数

以$2\pi$为周期的函数

如果一个函数以$2\pi$为周期，则它可以展开为形如$\frac{a0}{2} + \sum{n=1}^{\infty} (a_n cosnx + b_n sinnx)$，其中

若记$s(x) = \frac{a0}{2} + \sum{n=1}^{\infty} (a_n cosnx + b_n sinnx)$，则

以$2l$为周期的函数

如果一个函数以$2\pi$为周期，则它可以展开为形如$\frac{a0}{2} + \sum{n=1}^{\infty} (a_n cos \frac{n\pi}{l}x + b_n sin \frac{n\pi}{l})$，其中

若记若记$s(x) = \frac{a0}{2} + \sum{n=1}^{\infty} (a_n cos \frac{n\pi}{l}x + b_n sin \frac{n\pi}{l})$，则

偶函数

对于偶函数其傅立叶级数展开形式没有正弦项

奇函数

对于奇函数其傅立叶级数展开形式只有正弦项

复习一元函数泰勒展开

一元函数$f(x)$在点$x_0$展开：

从二元到多元

二元函数

首先看二元函数的二阶展开，对于二元函数$f(x, y)$在点$(x_0, y_0)$处展开式为：

转换为矩阵形式为：

推广到m元函数

由上的公式可以推出函数$f(x1,x_2,\ldots \space,x_m)$在点$(x{k1}, x{k2}, \ldots \space ,x{k2})$处展开的公式为：

若记

则上式可以写为:

麦克劳林公式是在$x=0$点处展开的泰勒公式

常用函数的麦克劳林公式的展开式：

1、指数函数

2、正弦函数

3、余弦函数

4、对数函数

5、幂函数

一个简单的记忆口诀: 幂指无负1，对数无阶乘，幂对起于1，首项都为正

几个重要的低阶展开的麦克劳林公式

1、$sinx = x - \frac{x^3}{3!} + O(x^3)$，$arcsinx = x + \frac{x^3}{3!} + O(x^3)$

2、$tanx = x + \frac{x^3}{3} + O(x^3)$，$arctanx = x - \frac{x^3}{3} + O(x^3)$

3、$cosx = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + O(x^4)$，$arccosx = \frac{\pi}{2} - x - \frac{x^3}{3!}-O(x^3)$

4、$ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} + O(x^3)$

5、$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + O(x^3)$

6、$(1+x)^{\alpha} = 1 + \alpha x + \frac{\alpha(\alpha - 1)}{2!} x^2 + O(x^2)$

利用上述公式可以得到一组“差函数的无穷小等价替换，例如：$x-sinx ～ \frac{x^3}{6}$​

这篇笔记用于记录经常在线性代数中用到的相关知识

线性代数基本术语

1、n阶矩阵即n阶方阵

2、如果矩阵A与矩阵B都是$m \times n$矩阵，就称A和B为同型矩阵

矩阵的乘法性质

1、结合律：$(AB)C=A(BC)$

2、数乘结合律：$k(AB) = (kA)B = A(kB)$，k为常数

3、分配律：$A(B+C) = AB+AC$

4、矩阵的乘法没有交换律，即一般有$AB \neq BA$，如果有$AB \neq BA$，称A与B是不可交换的；当$AB=BA$时，称A与B是可交换的。

5、即使有$A \neq 0(0矩阵)$，由$AB=BA$也不能退出$B=C$

6、$f(A) = ak A^k + a{k-1} A^{k-1} + \cdots + a_1 A + a_0 I,(a_0、a_1、\ldots 、a_n为常数)$，称为方阵A的k次多项式，如果有多项式$f(x)$与$g(x)$，则有$f(A)g(A) = g(A)f(A)$，注意都是A。但是一般情况下$f(A)g(B) \neq f(B)f(A)$。

7、$(A+\lambda I)^n = \sum_{k=0}^{n} \lambda^k A^{n-k}$

矩阵的转置的性质

1、$(A^T)^T = A$

2、$(A+B)^T = A^T + B^T$

3、$(kA)^T = k(A^T)$

4、$(AB)^T = B^T A^T$，$(A1 A_2 \cdots A_n)^T = {A_n}^T {A{n-1}}^T \cdots {A_1}^T$，$(A^n)^T = (A^T)^n$

5、若$A^T A = 0$，则$A = A^T = 0$

6、若$A^T = A$，则称A为对称矩阵；若$A^T = -A$，则称A为反称矩阵

8、实对称矩阵的n次方仍是实对称矩阵，证明：$A^n = (A^T)^n = (A^n)^T $

逆矩阵的性质

A为n阶矩阵，若存在n阶矩阵，使得$AB=BA=I$，则称A为可逆矩阵。A的可逆矩阵唯一，记为$A^{-1}$。

在使用处等变换求解矩阵的逆矩阵的过程中，如果使用行变换则只能全程使用行变换，如果使用列变换则只能全程使用列变换

1、$(A^{-1})^{-1} = A$

2、$(\lambda A)^{-1} = \frac{1}{\lambda} A^{-1}$

3、$(AB)^{-1} = B^{-1} A^{-1}$，$(A1 A_2 \cdots A_n) = {A_n}^{-1} {A{n-1}}^{-1} \cdots {A_1}^{-1}$，$(A^n)^{-1} = (A^{-1})^n$

4、

5、

6、$(E{ij})^{-1} = E{ij}$，$(E{i(c)})^{-1} = E{i(\frac{1}{c})}$，$(E{ij(c)})^{-1} = E{ij(-c)}$

行列式的性质

1、

2、

3、交换矩阵$A$的两行的到$A’$，则$|A’| = -|A|$，即有$|E_{ij}| = -1$

4、将矩阵$A$的某一行数乘k得到$A’$，则$|A’| = k|A|$，即有$|E_{i(c)} = C|$

5、将矩阵$A$的某一行的k倍加到另一行的到$A’$，则$|A’| = |A|$，即有$|E_{ij{c}}| = 1$

6、$|A^T| = |A|$

7、$|A^{-1}| = |A|^{-1}$

8、$|AB| = |A||B|$，继而有$|A^n| = |A|^n$

9、$|kA| = k^n |A|$，n为方阵的阶数

10、范德蒙行列式：

11、分块矩阵行列式

伴随矩阵性质

若方阵

则其伴随矩阵为：

其中$A{ij}$为$a{ij}$的代数余子式，注意$A^*$的下标排列方式

1、$\sum{k=1}^{n} a{ik} A_{jk} = 0$，($i \neq j; i, j = 1、2、\ldots \space、n$)，即矩阵的任一行（列）的元素乘以另一行(列)对应元的代数余子式之和为0

2、$AA^ = A^ A = |A|I$，$\implies A^{-1} = \frac{1}{|A|} A^*$

3、$(kA)^ = k^{n-1}A^$，n为方阵阶数

4、$(A^)^{-1} = (A^{-1})^$，$(A^T)^ = (A^)^T$

5、$|A^*| = |A|^{n-1}$，n为方阵阶数

6、$(AB)^ = B^ A^$，$(A^)^n = (A^n)^*$

克拉默法则

设n阶矩阵$A$可逆则线性方程组$Ax=b$有唯一解$(x_1,x_2, \space \ldots \space,x_n)^T$，其中$x_i = \frac{|A_i|}{A}$，$|A_i|$表示用b代替｜A｜中第j列得到的行列式

矩阵的秩

1、初等变换不改变矩阵的秩

2、设A为$m \times n$矩阵，则R(A) = r的充分必要条件是通过行初等变换(行变换和列变换能同时使用)能将A化为具有r个非零行的行阶梯行矩阵。这也是求解矩阵的秩的基本方法。

3、设$A$为n阶矩阵，则A可逆的充分必要条件是$R(A) = n$，即$A可逆 \iff R(A) = n$

4、$R(A) = R(A^T)$，$R(A^TA) = R(AA^T) = R(A)$

5、$R(A^*) = \begin{cases} n, \space 若R(A) = n \ 1, \space 若R(A)=n-1 \ 0, \space 若R(A) < n-1 \end{cases}$ ，这个性质的一个应用是证明A*为0矩阵，则只需要证明$R(A)< n-1$ 即可

6、设$A$为$m \times n$矩阵，$B$为$n \times s$矩阵，若$AB = 0$，则$R(A) + R(B) \leq n$

7、$R(AB) \leq min{R(A), \space R(B)}$，$R(A+B) \leq R(A) + R(B)$

8、若B为可逆矩阵，则$R(AB) = R(BA) = R(A)$

正交矩阵

矩阵相似

对于同型方阵A、B，若存在可逆矩阵Q，使得$Q^{-1}AQ = B$，记为$A～B$。